Playing audio - harder than it sounds!
I recently got to experience the fun of manually loading uncompressed audio and playing it on speakers. This seems like it would be easy and well documented. It isn't!!
Even though the sound at this level is basically just 'numbers telling you what the sound wave looks like' a lot of complexities aries, to the point that the most common response to queries seems to be 'install a third party library that handles it all for you'.
This would have been a sensible approach, but I kind of wanted to try coding my own sound mixer. Here's what I learned!

What is sound?
Sound comes in waves. A single tone for example looks like a bit like this:
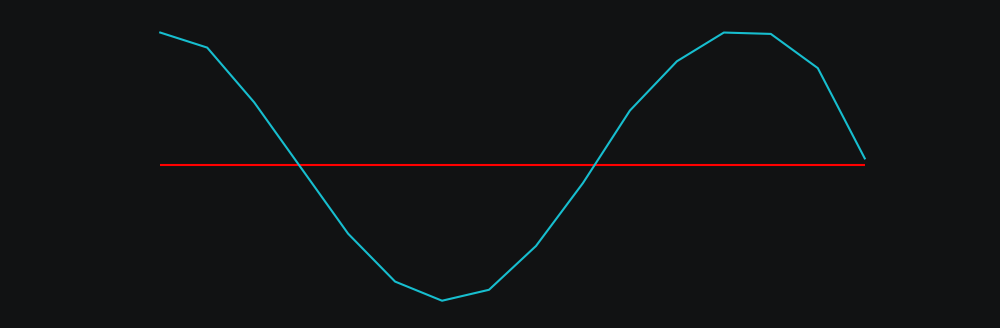
Lots of things look like waves, a fact that analog devices take advantage of to convert between sound and an signal - when the signal goes up, so does the magnet in a speaker*. The signal, be it a radio wave or a physical groove on a record, is an exact 'analog' of the sound itself!
Digital devices have the same basic theory, but instead of reading signal directly you're now interpreting it as a sequence of numbers!
The basic problem of reading numbers
For the sake of human readibility I'm going to talk in terms of decimal numbers ( 0 1 2 3 4 5 6 7 8 9 and any multi digit combinations). Computers work in binary ( 0 1 and any multi digit combinations) which is the exact same idea but with fewer numbers and more digits**.
Lets say Person A tells Person B something along the lines of:
 I have a list of numbers and it goes 123456
I have a list of numbers and it goes 123456
Now, what does that mean? Does it mean six one digit numbers?
 You mean as in 1, 2, 3, 4, 5, 6?
You mean as in 1, 2, 3, 4, 5, 6?
Or maybe three two digit numbers?
 You mean as in 12, 34, 56?
You mean as in 12, 34, 56?
Or even (stretching the definition of 'list') a single six digit number?
 You mean as in 123456 and nothing else?
You mean as in 123456 and nothing else?
The situation gets even more confusing when Person C gets involved! Imagine the following scenario!
 I have a list of numbers and it goes 123456
I have a list of numbers and it goes 123456
 Assuming you mean 12, 34, 56, I'm going to halve those two numbers to give 6, 17, 28 or 061728
Assuming you mean 12, 34, 56, I'm going to halve those two numbers to give 6, 17, 28 or 061728
 You mean as in 0, 6, 1, 7, 2, 8?
You mean as in 0, 6, 1, 7, 2, 8?
If the three characters (say audio input, application, and audio output) aren't all on the same page, you end up taking in a valid tone and pushing out what is essentially a wall of random noise!
A basic example
Let's dive right in with some examples of the following problem!
 I have a list of numbers and it goes 8999591947270584624280701000405002123444179688888999997978483525
I have a list of numbers and it goes 8999591947270584624280701000405002123444179688888999997978483525
 Umm...
Umm...
Now, how many ways can we interpret Person A's numbers as a sound wave? Well...
The naïve approach
What if we just straight up assume*** a list of single digit numbers
 I have a list of numbers and it goes 89995919 ...
I have a list of numbers and it goes 89995919 ...
 You mean as in 8 9 9 9 5 9 1 9 ...
You mean as in 8 9 9 9 5 9 1 9 ...
What does Person A's data look like if we try to turn it into a sound wave? Well...
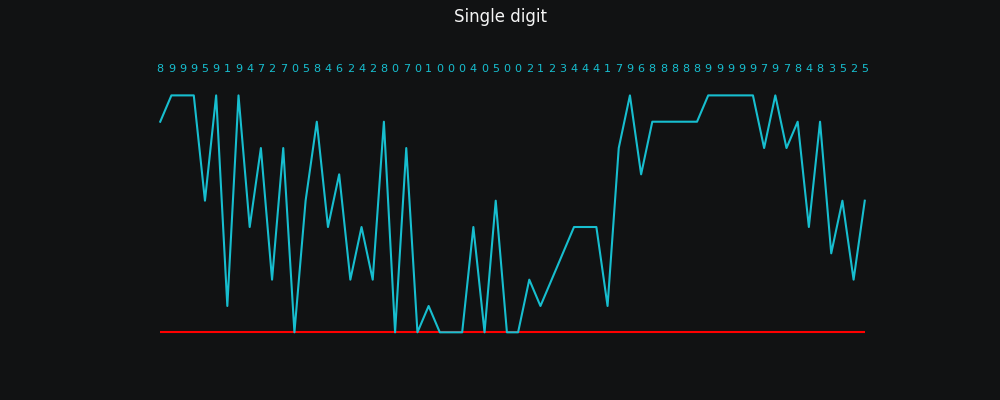
Clearly this interpretation leaves something to be desired! If you squint you might sort of see a wave shape, but this is pretty much co-incidental and the result is basically random noise!
The marginally less naïve approach
Okay, single digits don't work. How about double digits?
 I have a list of numbers and it goes 89995919 ...
I have a list of numbers and it goes 89995919 ...
 You mean as in 89 99 59 19 ...
You mean as in 89 99 59 19 ...
This looks like:
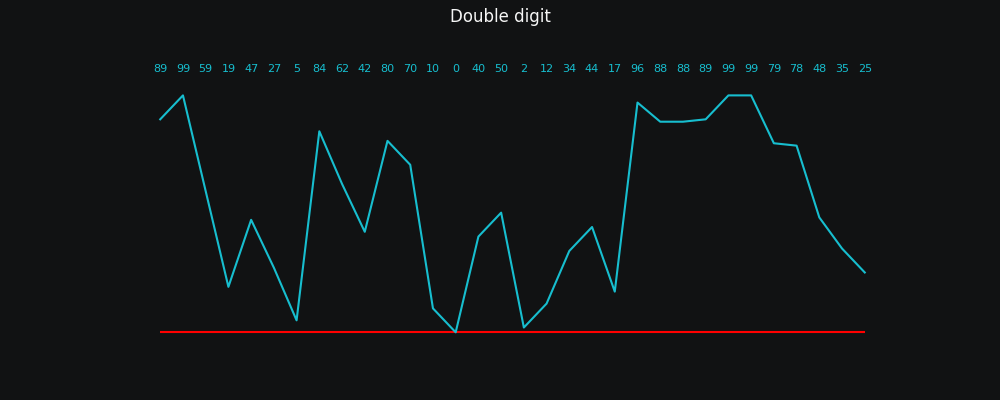
This is honestly just as bad as before! It looks marginally better due to there being less data, but the individual points are just as random.
Do quadruple digits fare any better?
 I have a list of numbers and it goes 89995919 ...
I have a list of numbers and it goes 89995919 ...
 You mean as in 8999 5919 ...
You mean as in 8999 5919 ...
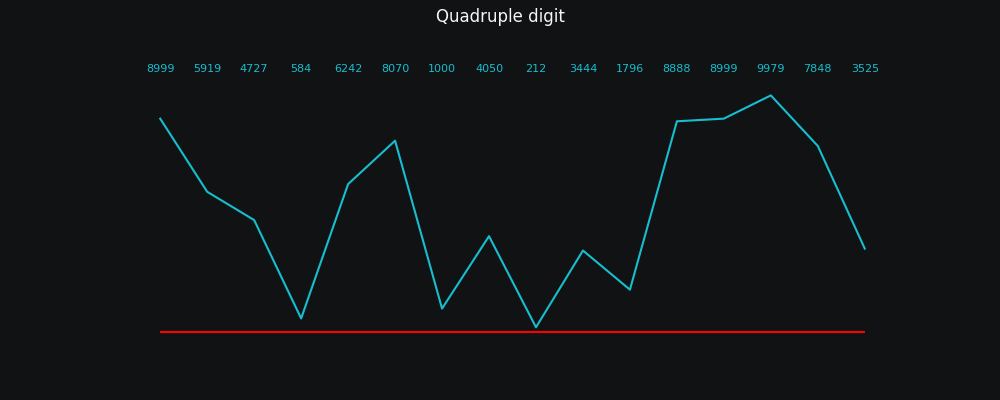
Again this looks superficially like an improvement due to there being fewer data points but is still just noise.
We remember that humans have two ears
There's another complication here that we've just been glossing over! Stereo sound means that a stream of data actually needs to encode two distinct sound waves - one for the left channel and one for the right****.
What if we assume that these two channels are interlaced, so instead of having MONO MONO MONO MONO MONO MONO we have LEFT RIGHT LEFT RIGHT LEFT RIGHT?
 I have a list of numbers and it goes 899959194727058462...
I have a list of numbers and it goes 899959194727058462...
 You mean as in 89 59 47 05... in my left ear and 99 19 27 84... in my right ear?
You mean as in 89 59 47 05... in my left ear and 99 19 27 84... in my right ear?
What we end up with is:
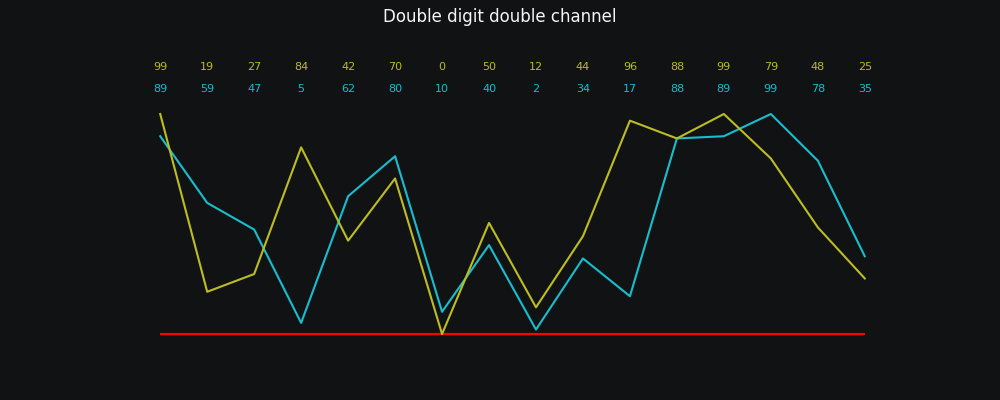
Okay, still not great, but there's one more complication that we've not talked about yet!
We remember that computers are weird
Endianness is a strange concept!
Imagine if one day a person decided:
 What if we reverse the order of digits, so that 123 means 'three hundred and twenty one' instead of 'one hundred and twenty three'
What if we reverse the order of digits, so that 123 means 'three hundred and twenty one' instead of 'one hundred and twenty three'
Imagine if this caught on, but not fully, so you had two different sets of people with different assumptions about what multi digit numbers should look like:
 I think that 123 means 'three hundred and twenty one'
I think that 123 means 'three hundred and twenty one'
 I think that 123 means 'one hundred and twenty three'
I think that 123 means 'one hundred and twenty three'
This sounds bizarre but writing numbers in reverse actually makes some calculations easier, and it's only a problem when some chump comes in to look at bytes at low level and expects them to be human readable.
Well, it's also a big problem when converting between systems.
Anyway, what happens when we combine this concept of 'endianness' with our two channel data?
 I have a list of numbers and it goes 899959194727058462...
I have a list of numbers and it goes 899959194727058462...
 You mean as in 98 95 74 50... in my left ear and 99 91 72 48... in my right ear?
You mean as in 98 95 74 50... in my left ear and 99 91 72 48... in my right ear?
What we end up with is:
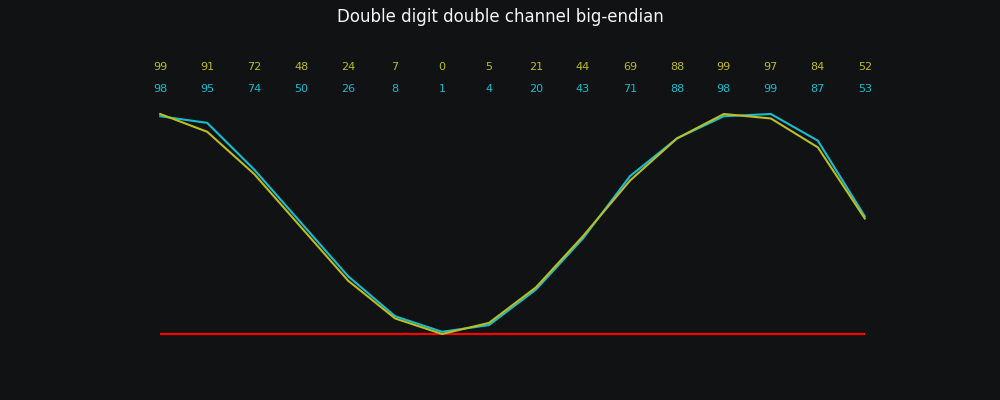
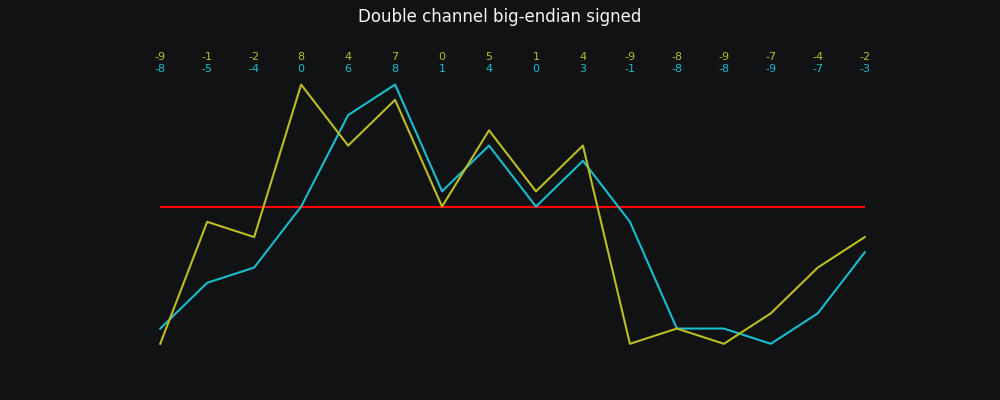
This... actually looks like the original sound wave! Well, with one important caveat:
We remember that negative numbers exist
Notice the red line at the bottom there? That's zero. Generally in the real world sounds oscillate around zero, going between positive and negative values.
Our numbers have so far been uniformly positive, so we don't have any of those negative values. There are a couple of things we could do. We could encode the plus or minus sign in the number (see Appendices) or just decide on some non-zero value for silence.
 I have a list of numbers and it goes 899959194727058462...
I have a list of numbers and it goes 899959194727058462...
 You mean as in 98 95 74 50... in my left ear and 99 91 72 48.. in my right ear, and also 50 is the value of dead silence?
You mean as in 98 95 74 50... in my left ear and 99 91 72 48.. in my right ear, and also 50 is the value of dead silence?
With this in mind, our final wave looks like:
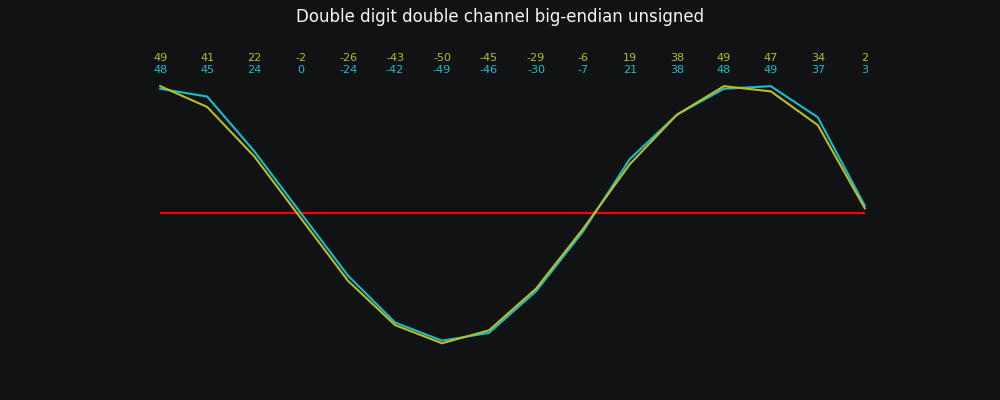
Which is pretty much what we wanted all along!
What have we learned
For me there are two big lessons here!
The first is that even relatively simple seeming tasks like bringing in uncompressed audio can have complication after complication! Just being able to consistently mix and play .wav sounds took four or five times longer than I would have assumed!
The level of complication is not an exaggeration - SDL defines 18 different audio formats for just raw data, and that is by no means a complete list since more could be added in future.
The second is that with a lot of computing problems, you can consistantly seem to be miles away from the solution until suddenly things click into place and work perfectly.
When digital sound became the standard, a big advantage was that it would (to grossly oversimplify) either completely work or completely break. A binary digit is either a 1 or a 0 - you can't wear down a record to turn a 1 into a slightly worse sounding 0.98 like you can with analog sound. If a sound plays at all, you can be confident that it's the best possible version of itself.
This kind of thing has the unfortunate side affect that 'slightly broken' sounds just as bad as 'completely broken' - even when we were most of the way there guessing the format we still had basically just white noise! It's easy to assume that you're nowhere near correct while standing right next to the solution.
The third, unspoken lesson is that I spent far too long trying to play a beep sound and I'm buggered if I'm not getting a post out of it.

* recording devices are the same but in reverse
** in practice computers like using bytes, which are groups of eight binary digits and let you represent numbers 0 through 15 (usually shown to human readers as 0 1 2 3 4 5 6 7 8 9 A B C D E F)
*** real world file formats come with metadata so we don't have to try and assume things
**** actaully we can encode any number of channels assuming someone's sound system is set up to play them all

Appendix A: Floating points!
This didn't really fit into the main discussion, but there are other ways to read numbers than as integers! What if we're using some form of 'scientific notation'?
 I have a list of numbers and it goes 89995919 ...
I have a list of numbers and it goes 89995919 ...
 You mean as in 8.99 × 10⁹ 5.91 × 10⁹ ...
You mean as in 8.99 × 10⁹ 5.91 × 10⁹ ...
This is similar to the four digits earlier, but we read the first three as a number and the last digit as an exponent (there are any number of ways you can represent bits as floating points in theory; in practice there are some common standards).
The useful thing about this way of representing sound is that it provides more precision for the important, perceptible differences at low volumes at the cost of less precision for less important small differences at high columes. The difference between 1 and 2 is much more important than the diference between 100001 and 100002.
Basically your low volume sounds are stealing bytes from high volume sounds that don't need them as much.
Does it work in our case?
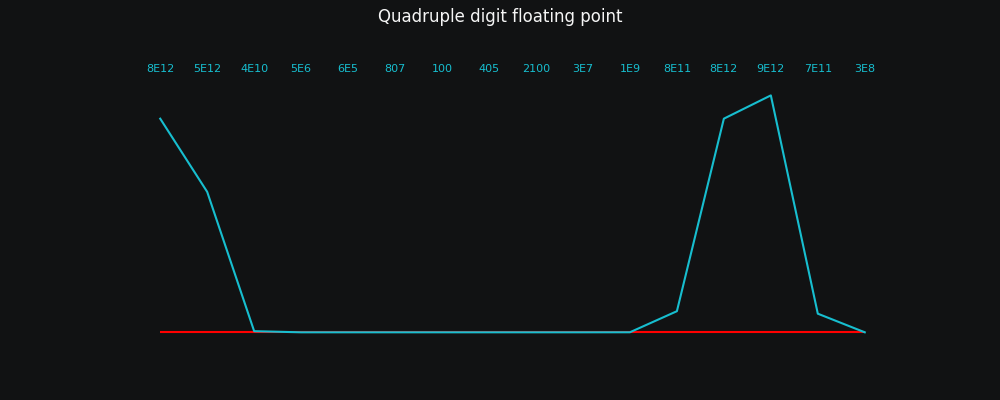
Nope.
Appendix B: Negative numbers!
In computing we talk about 'signed' and 'unsigned' numbers - basically numbers that are supposed to have a plus or minus sign and numbers that ignore the sign completely.
The simplest version of this is to have the first binary bit represent the sign. What if we do something really arbitrary and just make the following assumption:
 If the first digit is less than 5 it's a positive number, otherwise it's a negative number
If the first digit is less than 5 it's a positive number, otherwise it's a negative number
The result would be:
 I have a list of numbers and it goes 899959194727058462...
I have a list of numbers and it goes 899959194727058462...
 You mean as in -8 -5 -4 0... in my left ear and -9 -1 -2 8.. in my right ear?
You mean as in -8 -5 -4 0... in my left ear and -9 -1 -2 8.. in my right ear?
This is a pretty terrible way of representing negative numbers - even in binary where the first digit can either be 0 or 1 for plus or minus you have much better ways of encoding negative numbers. It's still yet enother complication to bear in mind though!

Inquisitive Dave
An adventure game with platforming elements, lots to explore and dark undertones!
| Status | In development |
| Author | EddyParanoia |
| Genre | Adventure, Platformer |
| Tags | 2D, Exploration, Multiple Endings, Pixel Art, Retro, Singleplayer |
| Languages | English |
| Accessibility | Color-blind friendly, Subtitles, Configurable controls |
More posts
- I talk about 1960s pulp sci fi series for 1046 consecutive words instead of doin...Aug 14, 2021
- Playing with fireAug 01, 2021
- Running through plants for an excessive amount of timeJul 12, 2021
- It's a bit like a massive ladderJul 05, 2021
- Tricking the playerJun 27, 2021
- Making a screen more appealingJun 20, 2021
- First major update!Jun 18, 2021

Leave a comment
Log in with itch.io to leave a comment.